Quelle der Infos: telegram/Links/YT
Das in der Natur beobachtete Fibonacci-Muster ist eine mathematische Folge, bei der jede Zahl die Summe der beiden vorhergehenden ist (z. B. 0, 1, 1, 2, 3, 5, 8…).
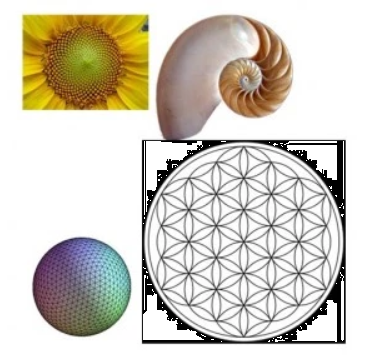
In der Natur spiegelt sich dieses Muster häufig in der Anordnung von Blättern, Blütenblättern und Samen bei Pflanzen sowie in den spiralförmigen Mustern von Muscheln und der Verzweigung von Bäumen wider.
Die inhärente Effizienz dieses Musters trägt zur optimalen Verteilung von Ressourcen und zum Wachstum bei und macht es zu einem wiederkehrenden und visuell auffälligen Phänomen in verschiedenen lebenden Organismen.
🔸mehr bei t.me/Lebens_Filou_Sophien
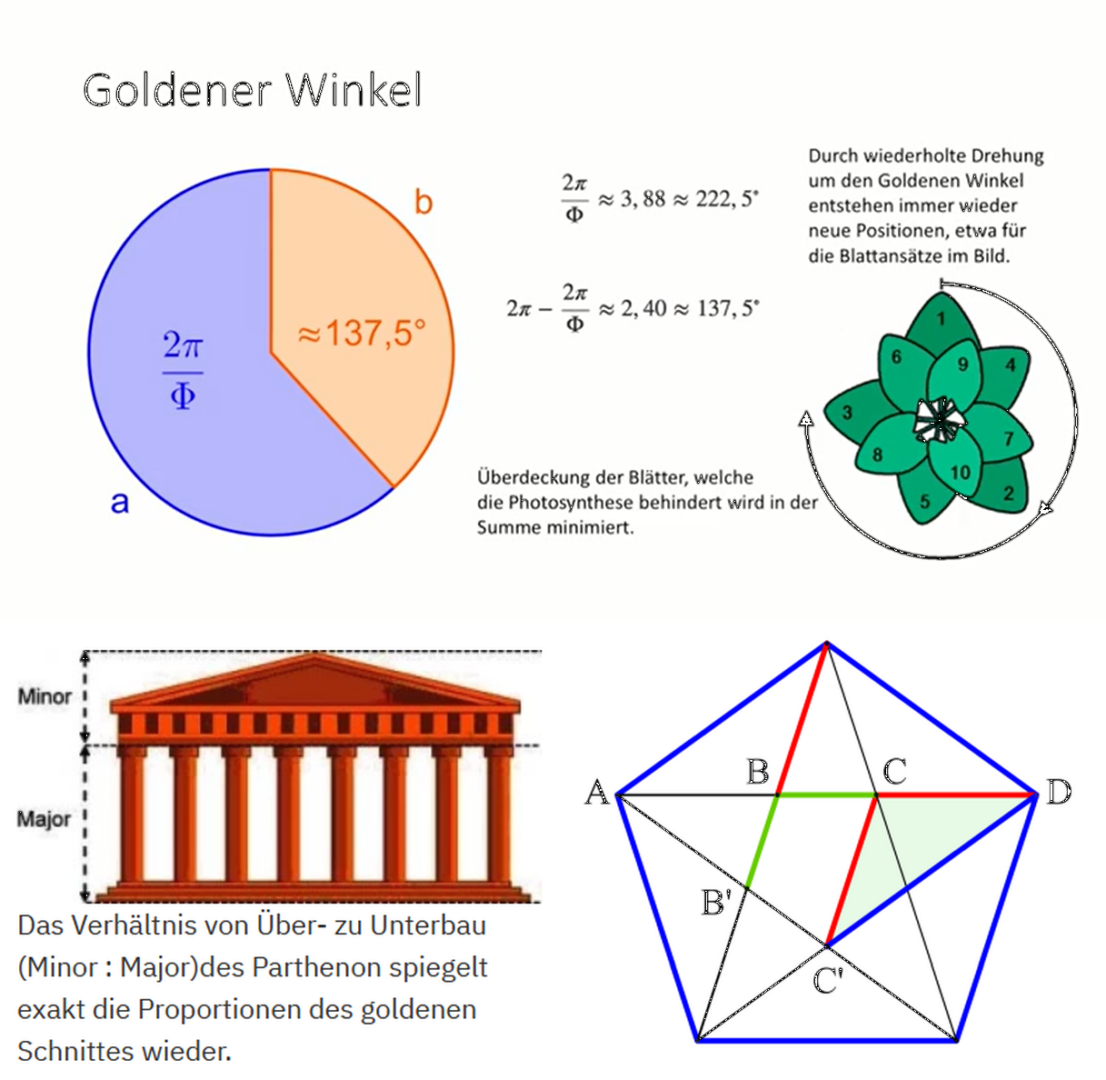
Verhältnisse: Große Zahl / Kleine Zahl = 1,618 (Majuskel) – bzw. umgekehrt Kleine Zahl / Große Zahl = 0,618 (Minuskel)!
Man beachte die 618!
Diese Verhältnisse gelten auch bei großen Fibonacci-Zahlen !
Die Zahl wird mit dem griechischen Buchstaben Phi Φ bezeichnet und entspricht etwa einem Verhältnis von 1 : 1,618, man nennt sie auch die Goldene Zahl!
Majuskel: Φ, Minuskel: φ, ϕ
Wenn man zwei aufeinander folgende Fibonacci-Zahlen teilt, erhält man eine Zahl, die sich dem Goldenen Schnitt annähert, d. h. man erhält die beste Annäherung an den Goldenen Schnitt, wenn man die größt möglichen Fibonacci-Zahlen miteinander teilt!

Es gäbe zwei Strecken. Teilt man die größere Strecke durch die kleinere, und es kommt 1,618 raus, stehen die beiden Strecken im goldenen Verhältnis zueinander. Diese Zahl wird der goldene Schnitt oder auch die goldene Zahl genannt. Diese Zahl kommt immer dann raus, wenn die größere Strecke durch die kleinere Strecke, das gleiche ist wie die Ganze Strecke durch die größere Strecke.
Also das Verhältnis von a zum Ganzen, muss genauso sein wie das Verhältnis von b zu a, dann hat man den goldenen Schnitt. a/b = (a+b)/a = 1,6180339887… Will man den reziproken Wert entsteht 0,6180339887… Einzigartig!